NumPy 使用

介绍

数组对象：numpy.ndarray

参考资料

np.argsort()
np.sort()

# 找到 2D 数组 arr 最小值的对应行、列索引
i, j = np.unravel_index(np.argmin(arr, axis=None), arr.shape)

# 数值积分函数；通过梯形法则（trapezoidal rule）计算定积分
np.trapz()

# 按照第 2 列元素进行排序
new_arr = arr[arr[:, 1].argsort()]

使用

工具

Eigen3 转换成 numpy：GitHub - jrl-umi3218/Eigen3ToPython: Provide Eigen3 to numpy conversion

数组创建

初始化 numpy 数组时，可以进行预分配

import numpy as np

# 从列表创建
np.array([1, 2, 3])

# 从内置函数创建
np.eye()                # 单位阵
np.zeros()              # 全为 0
np.ones()               # 全为 1
np.full()               # 填充
np.arange()             # 范围
np.linspace()           # 等差
np.logspace()           # 等比
np.fromstring()         # 从字符串提取数据

# 随机
np.random.rand()        # 0-1 随机小数
np.random.randint()     # 随机整数
np.random.normal()      # 正态分布随机数
np.random.uniform()     # 均匀分布随机数


# 数组元素是类浮点数的字符串时
a = [f"{x:.1f}" for x in range(1, 10)]
array = np.array(a, dtype=float)

属性

dtype                   # 数组元素数据类型
shape                   # 数组形状
ndim                    # 数组维度
size                    # 数组元素个数

索引

普通索引、切片索引、布尔索引

1 2	arr[[1, 2], [1, 2]] # 索引的是 2 个元素，分别是 [1][1] 和 [2][2] arr[np.ix_([1, 2], [1, 2])] # 索引的是子 2 维数组，即第 2、3 行与列的交叉数组

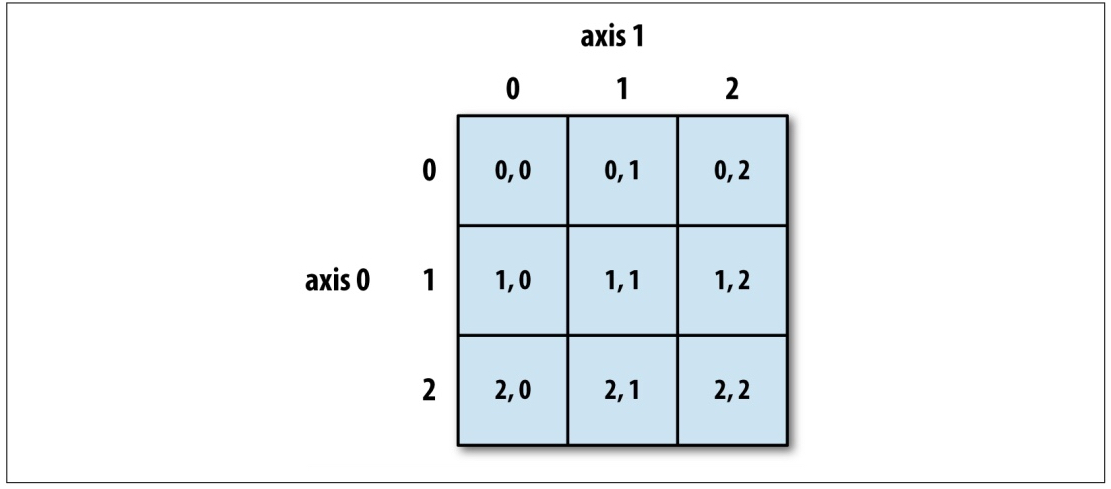
二维数组的普通索引

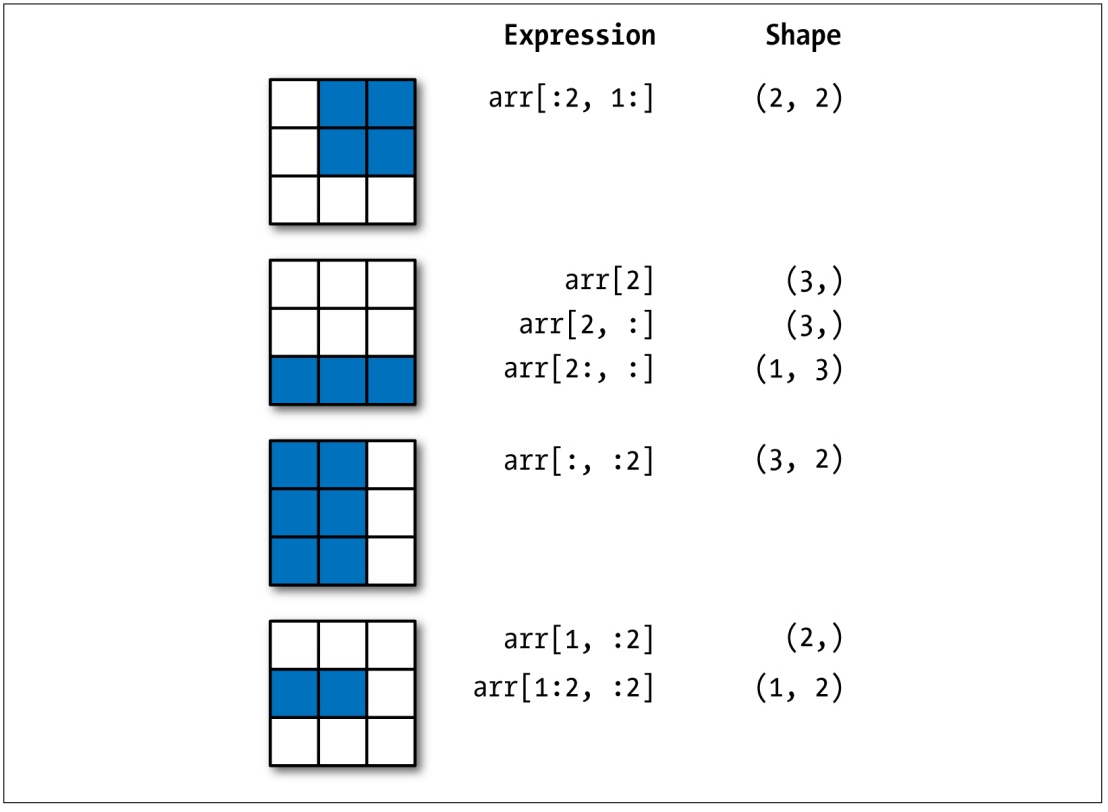
二维数组的切片索引

数学运算

*                       # 数组乘法，元素相乘
np.square()             # 平方
np.sqrt()               # 平方根
np.cbrt()               # 立方根
np.log2()               # 对数计算
np.round()              # 保留小数位数

np.set_printoptions(suppress=True)      # 不使用科学计数法

通用一元函数：参数是一个数组对象，函数会对数组进行元素级的处理

abs / fabs                       # 绝对值
sqrt                             # 平方根
square                           # 平方
exp                              # e 指数幂
log / log10 / log2               # 对数函数
sign                             # 符号函数
ceil / floor                     # 向上/下取整
isnan                            # 返回布尔数组；NaN 为 True，非 NaN 为 False
isfinite / isinf                 # 判断数值是否为无穷大
cos / cosh / sin                 # 三角函数
sinh / tan / tanh                # 三角函数
arccos / arccosh / arcsin        # 反三角函数
arcsinh / arctan / arctanh       # 反三角函数
rint / round                     # 四舍五入

通用二元函数：参数是两个数组对象，函数会对两个数组中的对应元素进行运算

np.allclose(x, y)    # 检查数组 x 和 y 元素是否几乎相等
np.dot(x, y)         # 点积运算
np.inner(x, y)       # 内积运算
np.cross(x, y)       # 叉积运算
intersect1d(x, y)    # 交集

统计

axis 参数指定运算沿着哪一个轴来执行，不指定时为对整个数组

np.sum()     # 加和
np.mean()    # 算术平均值
np.min()     # 最小值
np.max()     # 最大值
np.std()     # 标准差
np.var()     # 方差

其他常用函数

函数调用：

方式 1：Numpy 模块本身的函数（即 np.function()），如统计相关函数
方式 2：通过数组对象本身的方法（即 array.method()），如数组创建函数，数学和线性代数操作等

np.copy()             # 拷贝

np.diff()

np.reshape()          # 改变数组形状；当一个维度的参数值为 -1 时，会自动推断出该维度的值
np.all()              # 判断数组是否所有元素都是 True
np.any()              # 判断数组是否有为 True 的元素

tolist()              # 转换成 list 类型


np.flatten()          # 扁平化

np.unique()           # 去重；返回的元素是排序过的（从小到大）
# 参数
return_count=True     # 返回相同元素的数目

np.hstack()           # 横向堆叠多个数组构成新数组
np.vstack()           # 纵向堆叠多个数组构成新数组
np.append()           # 追加元素
np.insert()           # 插入元素
np.where()            # 条件查询
np.argwhere()         # 满足条件的元素索引

np.remainder()        # 计算数组余数

np.isclose()          # 比较两个数值是否在某个容忍范围内接近相等
# 参数
rtol                  # 相对容忍值
atol                  # 绝对容忍值

IO

查看 NumPy npy npz 格式文件的 VSCode 插件：vscode-numpy-viewer
npy、npz 格式区别：npy 只能存单个数组，npz 可存多个数组

np.save("*.npy", arr)   # 存储到 npy 文件格式
np.savez("*.npz", ...)  # 存储到 npz 文件格式
*args        # 位置参数，保存的数组将按顺序存储，名称为 arr_0 ...
**kwds       # 关键字参数，给数组指定名称

# 用关键字参数将数组存储到 npz 文件
kwargs = {}
for i in range(3):
    kwargs[f"array_{i}"] = ...
    np.savez("*.npz", **kwargs)

np.load(file)           # 导入 npy npz 文件

arr = np.load("*.npy")

data = np.load("*.npz")
data.files              # 返回存储数组的名称列表
data["arr_0"]

np.dump()               # 保存数组到二进制文件中
np.tofile()             # 将数组写入文件中

np.savetxt()
np.loadtxt()

# 从普通文本中读取数据
np.genfromtxt()

线性代数

linalg 模块

.T                              # 转置
np.transpose()                  # 同上

@                               # 矩阵乘法
np.matmul()                     # 同上
np.dot()                        # 矩阵 1D，点积；2D，矩阵相乘

np.outer()                      # 1*n 一维列向量与 m*1 一维行向量外积得到 m*n 矩阵
np.triu(..., k=...)             # 提取上三角矩阵；k 为偏移量
arr.trace()                     # 对角线元素和
np.linalg.trace()               # 对角线元素和
np.linalg.matrix_rank()         # 矩阵的秩
np.linalg.inv()                 # 求逆
np.linalg.det()                 # 求行列式
np.linalg.eig()                 # 计算特征值、特征向量
np.linalg.qr()                  # QR 分解
np.linalg.svd()                 # 奇异值分解
np.linalg.solve()               # 解线性方程组
np.linalg.norm(x, ord="fro")    # 范数 ord="fro" F-范数

多项式

# 方式 1
p = np.poly1d((2, 3, 1))

# 方式 2
from numpy.polynomial import Polynomial

p = Polynomial((2, 3, 1))


coeffs  # 获取多项式系数
coefficients

roots  # 获取多项式的根

deriv()  # 求导
integ()  # 不定积分


polyfit(x, y, deg)        # n 次多项式拟合；返回多项式的系数
# 参数
deg                       # 多项式阶数

np.polyval()